

Recurso Didáctico Digital
Unidad 5: métodos de evaluación de proyectos de inversión de la UA Finanzas Empresariales
- Introducción
- 5.1 Los proyectos de inversión
- 5.2 Proceso de preparación y evaluación de proyectos
- 5.3 Métodos de evaluación financiera de proyectos de inversión
- 5.3.1 Método del período de recuperación de la inversión (PRI)
- 5.3.2 Método de rendimiento anual promedio (RAP)
- 5.3.3 Índice de rentabilidad
- 5.3.4 Valor presente neto (VPN) o valor actual neto (VAN)
- 5.3.5 Tasa interna de rendimiento (TIR)
- Actividades de aprendizaje
- Evaluación
- Cierre
5.3.5 Tasa interna de rendimiento (TIR)
La TIR es la tasa de descuento que hace que el valor presente de los flujos netos de efectivo generados por un proyecto sea igual a la inversión inicial requerida; es decir, es la tasa que provoca que el VPN de un proyecto sea igual a cero.
Su fórmula es:
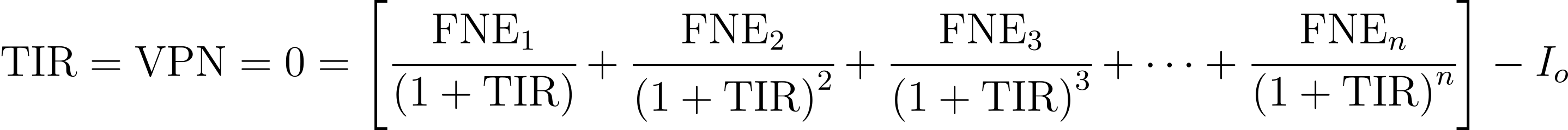
Donde:
- TIR = Tasa interna de rendimiento
- VPN = Valor presente neto
- FNE = Flujo neto de efectivo
- Io = Inversión inicial requerida
- n = Número de periodos de vida del proyecto (tiempo de vida)
El valor que satisfaga la ecuación anterior será el que ocasione que la suma de los flujos netos de efectivo descontados sea igual a la inversión inicial requerida para realizar el proyecto. Cabe señalar la relación inversa que existe entre la TIR y el VPN: cuando se incrementa la TIR, disminuye el VPN, y cuando disminuye la TIR, se incrementa el VPN.
No existe una forma directa de obtener el valor de la TIR, es necesario encontrarla mediante prueba y error. Sin embargo, en Excel tenemos la función financiera TIR que permite calcular el valor de manera automática.
Continuando con nuestro ejemplo: El proyecto “A” requiere una inversión de $10,000 pesos, los flujos netos de efectivo (FNE) esperados para los años del 1 al 5 son $2,500, $3,200, $4,100, $5,300 y $5,000 respectivamente; vamos a calcular la TIR.
Realicemos el primer ensayo proponiendo un valor para la TIR del 20%, con este valor nos concentraremos en la suma de los flujos netos descontados (en el ejemplo, corresponde a los períodos del 1 al 5) los cuales tiene que dar el valor de la inversión inicial.
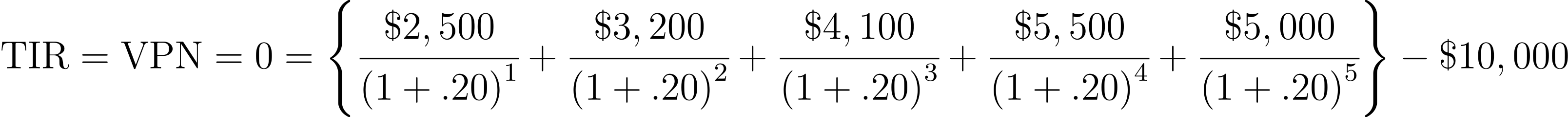
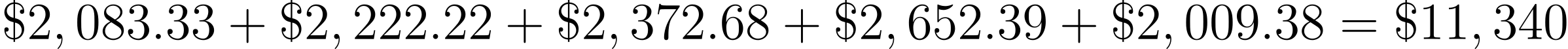
Como podemos observar el valor que obtenemos de la suma de los flujos descontados es superior a la de la inversión inicial, por lo que ahora propondremos un valor mayor para la TIR; proponemos 25%
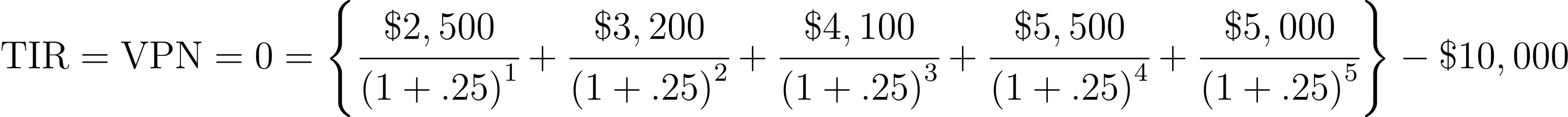
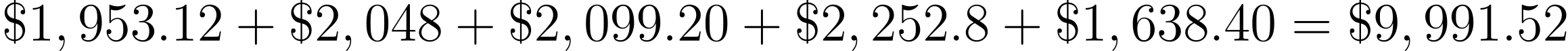
Con el nuevo valor propuesto ahora la suma de los flujos netos descontados está por debajo del valor de la inversión inicial lo cual quiere decir que el valor de la TIR que buscando se encuentra entre 20% y 25%, por lo que procederemos a interpolar para encontrar un valor más preciso.
Para interpolar vamos a emplear una matriz con 3 columnas y 4 renglones (tabla 6).
Primer renglón
Colocar el valor que obtuvimos de la suma de los flujos descontados $11,340 (columnas 2 y 3) cuando propusimos la tasa del 20% (columna 1).
Segundo renglón
Únicamente en la columna 3 colocar el valor de la inversión.
Tercer renglón
En la columna 2 registrar la suma de los flujos netos de efectivo descontados que fueron de $9,991.52 cuando se propuso la tasa del 25% (columna 1).
Cuarto renglón
Se restan los valores registrados en las columnas 2 y 3.
| 1 | 2 | 3 | |
| 1 | 20% | $11,340 | $11,340 |
| 2 | r% | $10,000 | |
| 3 | 25% | $9,991.52 | |
| 4 | $1,348.48 | $1,340 |
Fuente: Rodríguez, E., Hernández, J. y Jiménez, Y (2021), con base en las referencias consultadas.
Ya que obtenemos el valor de las restas correspondientes, dividimos el resultado de la columna 3 entre el resultado de la columna 2. Dicho resultado se multiplica por la diferencia que hay entre las tasas propuestas (20 - 25 = 5), que en este caso es de 5, a este resultado le sumamos la tasa propuesta con el menor valor, para nuestro ejemplo es 20% y así el resultado de la TIR es del 24.97%.
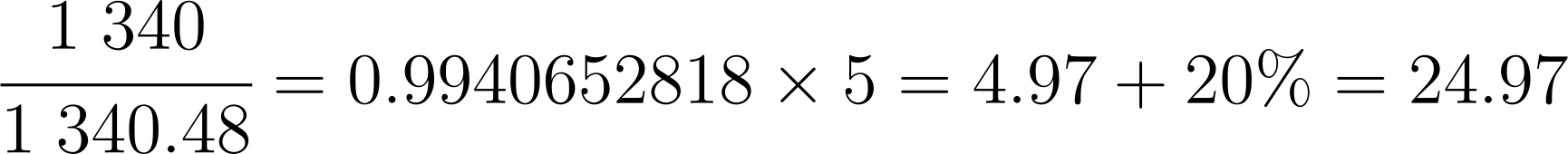
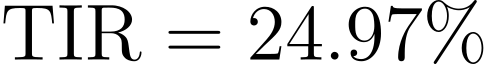
Criterios de decisión:
Como el valor que obtuvimos de la TIR es superior al valor de la tasa mínima de aceptación del proyecto, el proyecto se deberá aceptar.
Cada uno de los métodos de evaluación expuestos proporcionan información diferente con relación a un proyecto y puede ser útil para evaluar un proyecto de inversión específico. En algunas ocasiones las decisiones de presupuesto de capital se basan en la aplicación simultánea de uno o más métodos, pero por lo general, los dos métodos más utilizados por las empresas para evaluar sus proyectos de inversión son el VPN y la TIR, ya que ambos consideran el valor de dinero en el tiempo y todos los flujos de efectivo que se espera que genere el proyecto durante su tiempo de vida.
Una diferencia importante entre el método del VPN y el de la TIR es que el primero supone que los flujos de efectivo netos generados por el proyecto se reinvierten al costo de capital; mientras que el supuesto del segundo método es que los flujos de efectivo netos se reinvierten a la tasa interna de rendimiento; sin embargo, en los dos casos el supuesto de la tasa de reinversión está implícito en el método, aunque para muchos el supuesto del VPN es más acertado, por lo que este método se considera mejor que el de la TIR.
Por último, es importante mencionar que una de las etapas más difíciles del proceso de evaluación de proyectos no es la elección y aplicación de un método de evaluación sino la estimación de los flujos de efectivo netos que se espera obtener.
Ejercicio
Resuelve el siguiente ejercicio:


